
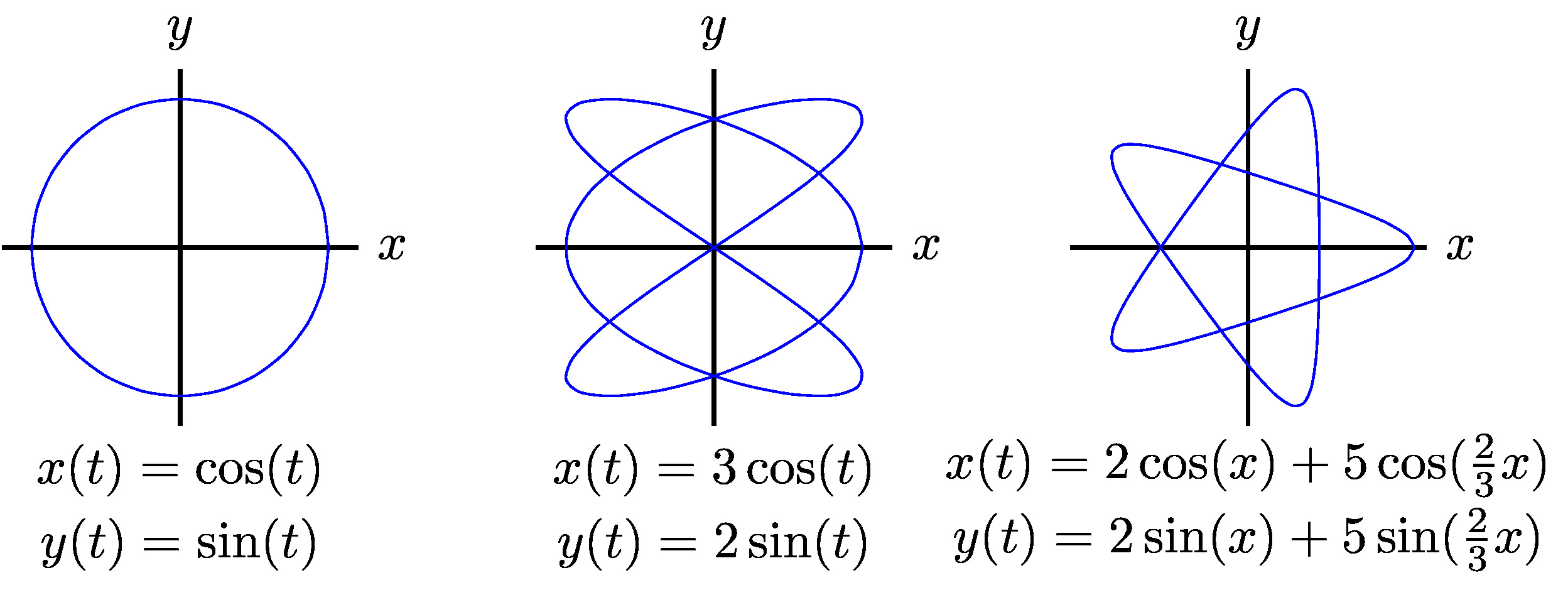

We can determine the functions for x ( t ) Therefore, each point on the graph corresponds to a value of Earth’s position as a function of time. Then each x value on the graph is a value of position as a function of time, and each y value is also a value of position as a function of time. If we superimpose coordinate axes over this graph, then we can assign ordered pairs to each point on the ellipse ( ). Is one of the foci of the ellipse the other focus is occupied by the Sun. depicts Earth’s orbit around the Sun during one year. We study this idea in more detail in Conic Sections.

According to Kepler’s laws of planetary motion, the shape of the orbit is elliptical, with the Sun at one focus of the ellipse.
#Parametric equations calculus examples full
After one full year, we are back where we started, and a new year begins. As Earth revolves around the Sun, its physical location changes relative to the Sun. The number of the day in a year can be considered a variable that determines Earth’s position in its orbit. Then, for example, day 31 is January 31, day 59 is February 28, and so on. On January 1 of each year, the physical location of Earth with respect to the Sun is nearly the same, except for leap years, when the lag introduced by the extra 1 4ĭay of orbiting time is built into the calendar. Our year lasts approximately 365.25 days, but for this discussion we will use 365 days. Parametric Equations and Their GraphsĬonsider the orbit of Earth around the Sun. Then x and y are defined as functions of time, and ( x ( t ), y ( t ) )Ĭan describe the position in the plane of a given object as it moves along a curved path. For example, if the parameter is t (a common choice), then t might represent time. The parameter is an independent variable that both x and y depend on, and as the parameter increases, the values of x and y trace out a path along a plane curve. In the two-dimensional coordinate system, parametric equations are useful for describing curves that are not necessarily functions. In this section we examine parametric equations and their graphs. Recognize the parametric equations of a cycloid.Recognize the parametric equations of basic curves, such as a line and a circle.Convert the parametric equations of a curve into the form.Plot a curve described by parametric equations.


 0 kommentar(er)
0 kommentar(er)
